|

あれやこれや
新国立劇場で二期会の魔笛を鑑賞してきたのですが,話が長くなるので後日.今日
はSS氏のワザの続きです.今回こそ本当に役に立つはず.多分,昔は市民権のあ
った手法でSS氏独特のものではなかったと思うのですが,私はSS氏に教えを頂い
たので一連のSS氏の技法の1つとして取り上げます.
先ずちょっと中学校の復習.例えば水100mLとメタノール100mLを混ぜると,全体の
容量は200mLにはならず,ずっと小さくなるということは覚えておられますね.同じよ
うに水100mLと10%食塩水100mLを混ぜても厳密には200mLにはならないのです.こ
の辺の話は面倒なので(厄介な理屈があります),そういうものだということにしてお
きます.だから厳密さを要する場合は以下のSS氏の技法は成り立ちませんが,水と
食塩水を混合した場合,全体の容量も足し算したものと同じとして大勢に影響がな
いという場面(普通はこれで問題はない)では,実に便利な手法なのです.今の大学
では実用的ではあっても理論的ではないということで教えてはいない様ですので,ご
参考までに書いておきます.
a%の水溶液Aとb%の水溶液Bを混合してc%の水溶液を作りたい.A液,B液それぞれ
何mLずつ採取したらよいでしょうか? こんな問題は現実に良くあるはずです.例え
ば20%の食塩水を希釈して7%の食塩水にしたい.さてどうしましょうか.簡単簡単,子
供でも分かります.では水で希釈する代わりに1%の食塩水で希釈することにしたら.
こうなると厳密に計算するのはお手上げですが,堅いことを言わなければ簡単な方
法があるのです.
上のA液とB液の問題では,A液を(a-c)mL,B液を(c-b)mL混ぜれば良いだけなので
す.何か狐につままれたようですが,それぞれの液の採取量は目的濃度との差の
数値だけの容量を混ぜればよい.本来不正な%間の引き算で単位が気になります
が,比例の問題なので気にしないこと.
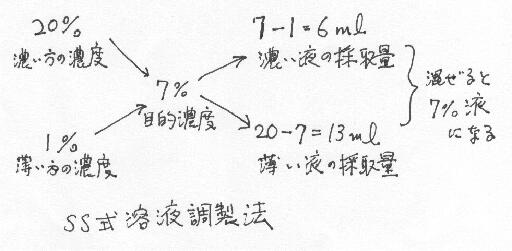
具体的に見ると,1%の食塩水で希釈する上記の例では,aが20%で,bが1%.目的濃
度cは当然7%ですので20%食塩水を(20-7)=13mL,これに1%食塩水を(7-1)=6mL加え
れば,ハイできあがり.簡単でしょ.図に示すと次のようになります.昔は交差法と言
ったはずですが,冒頭の通り厳密性を欠いていますので今は市民権がないのか・・・
法とも呼ばれず,学校でも教えない幻の技法になっているようです.でも,実用性は
十分.実生活の場でも是非活用していただきたいと思います.
|
|
|

|